好奇心是人类学习和探究的最初动力。在应试教育体制下，并不缺乏勤奋好学的学生，而是缺少对未知世界充满好奇心并勇于探索的学生。大学教学要能够唤起学生的好奇心，激发学生主动探究科学知识的热情，引导学生将创造性潜能释放出来。大学课堂必须要从传统的“以教师为中心”向“以学生的学习为中心”变革。以我主讲的《高等数学》为例，我始终坚持将“让学生学会搭建知识体系、学会自主学习”作为教学的终极目标，积极推进高等数学课程改革。在课程改革的进程中，围绕“如何发掘学生对数学的热爱、如何保护学生的好奇之心、如何在教学中培养学生严谨的思维习惯、如何启发学生思考数学的本质、如何帮助学生搭建知识体系”等一系列问题展开探索和实践，逐渐在学习平台搭建、教学模式改革、学生学习力促进、教师自我教育等方面形成了经验和成果。

作业是高数学习过程中的一个重要环节。基于多年的教学经验，我意识到“作业批改、作业完成质量、学生作业分析”是教学中相对薄弱的环节，如不加以重视，则会对学生的学习效果产生直接的负面影响。基于此，我在课程教学中增加了一些辅助性的教学手段，一是采用思维导图教学法，帮助学生建立系统完整的知识框架体系,有利于学生在完成作业时综合利用知识来解答问题。二是对学生作业中的易错点进行分析，既能促进学生对难点知识的理解和掌握，也训练了学生思维的严谨性。三是注重助教的作业反馈，点评解题过程，鼓励进步，提高学生的作业质量。

除此之外，我与香港科技大学数学系合作搭建了上海交通大学高等数学Classviva在线教学平台。该平台支持Latex，有强大的后台数据分析功能。该平台支持学生作业的提交、自评、互评等功能，能够追踪学生的学习习惯和学习效果。该平台在解决作业问题的同时，引入同伴式学习，既有助于提升学生的学习兴趣，又能够培养学生的主动学习能力。

（一）教学模式匹配学习模式

近年来，随着高校专业设置的不断细化，理工、经管、医农和人文等专业对高等数学课的要求有明显的变化与差异。加之在线学习资源的多元化、选课学生的多层次化，传统的高等数学教学模式很难满足当前学科专业发展的要求，也难以适应新生代大学生的学习需求。故而，高等数学教学改革势在必行。为此，上海交通大学数学科学学院对高等数学实行教学改革，实施“大班教学，小班辅导”的授课模式。从教师教学的视角来看，“大班教学，小班辅导”是一种合作型的教学模式；从学生学习的角度而言，它是一种“反刍式”学习模式，学生通过大班教学获得理论知识，通过小班辅导实现对知识的加深和拓展。这一学习模式比较符合学习规律，学生的接受度比较高。

为匹配学生的反刍式学习模式，我将教学内容进行了重构，分为基本授课内容和加深拓展内容两部分，并将原有教学模式同步改变为“大班教学+小班辅导”模式。“大班教学”的主要任务是传授课程的主干内容，强调知识体系的建立和知识点的逻辑性。“小班辅导”既要加深学生对大班教学内容的理解，更要关注学生存在的个性化学习问题，通过弹性地调整课堂内容来适应学生的学习需求，通过开展课程相关的研讨来回应学生的疑难点。例如，“数列极限”这一基础概念，基本授课内容包括极限的定义、性质、归并定理等；加深拓展内容包括不收敛、借助任意性和存在性构造数列和子列、归并定理的第二种推导方式等。基本授课内容可以自成体系，而加深拓展内容的深度则依赖于小班学生的掌握程度。教学内容的重构，既能够避免学生因高数太难而压力重重，又能够让学生获得学习成就感。

总之，“大班教学，小班辅导”是将以教师为主体和以学生为主体的两种教学模式有机结合，达到了共性与个性的统一，促使教学效果的最大化。

（二）问题驱动，做一个优秀的课程设计者

当代大学生思维活跃、视野开阔，对老师提出的问题能够积极思考，主动探求。例如，按照教学要求，不可积的函数讲解五类即可，但我在上课时会提及“事实上还有很多不可积的函数”。于是，每年都有学生主动补充其他的不可积函数，发到课程微信群里，展开积极讨论。学生积极的探索态度给我的课堂教学也提出了更高的要求，我不得不思考如何让课堂更具吸引力，以抓住学生的思维，促使学生自主探索。同时思考如何成为一个优秀的课程设计者，为学生在庞杂的信息面前理清思路，使其学会辨析、学会学习。

问题驱动式教学，突出了“教”与“学”的融合，教师通过一系列的问题，引导学生的思维层层深入，这样的教学方式有利于激发学生对数学的热爱，培养学生的高阶思维和探究精神，帮助学生提升学习自觉性和主动性。例如，我在第一节课时就提出了促使微积分产生的四类科学问题，让问题贯穿课程教学始终；讲隐函数和反函数概念的时候提出两个函数的存在性问题，该问题延续到课程的第二学期。这都有利于学生带着问题进行学习，在问题的驱动下一步步地探究答案。同时，问题的设置也加强了课程内容之间的横向联系，提升了课程的粘性，让学生卷入到整个课程的探究中。

（三）用辩证统一的思想审视高数，讲好高数这个故事

好的课程都会有好的故事，教师是故事的讲述者。现行的教材和教辅，其结构和内容基本上无懈可击，但是很多概念看起来却比较孤立，使得知识结构以树状呈现。事实上，当我们使用辩证统一的思想去审视高等数学时，即会发现不同的知识点也存在相似的结构、相似的研究方法，这些知识点之间蕴藏着深层次的逻辑关系。受此思想的指引，我不断地挖掘高数概念之间的逻辑关系，从而把树状的知识点连接起来，形成网状结构，使得整个课程内容的故事性更强，讲课时就可以从完整的故事视角进行叙述，有利于学生结构化思维的养成，促进其对知识的自我建构。

例如，“广义积分与级数理论”、“实数连续性理论与反证法的选择”这两组概念看起来是孤立的，但进行对比分析后可发现，广义积分与级数理论之间存在内在联系；实数连续性理论的证明中反证法的选择有章可循。再比如，“初等函数”这一概念在教材中只是简单提到定义，并没有阐述这个概念对课程的深刻影响，进一步挖掘即可发现，初等函数概念的拆分对学生理解高数的框架结构起着很重要的作用。在辩证统一的思想指引下，把高数的故事讲圆、讲精彩，使得高数教学成为一门艺术，就可以激发学生的好奇心和求知欲。

学生需要进行科学的学习。科学的学习不仅需要学生自悟，也需要教师立足于课程本身的特点给予学习方法上的指导，这将使得学生的学习事半功倍。在教学中发现学生的学习存在问题时，我都会及时提供方法上的帮助。

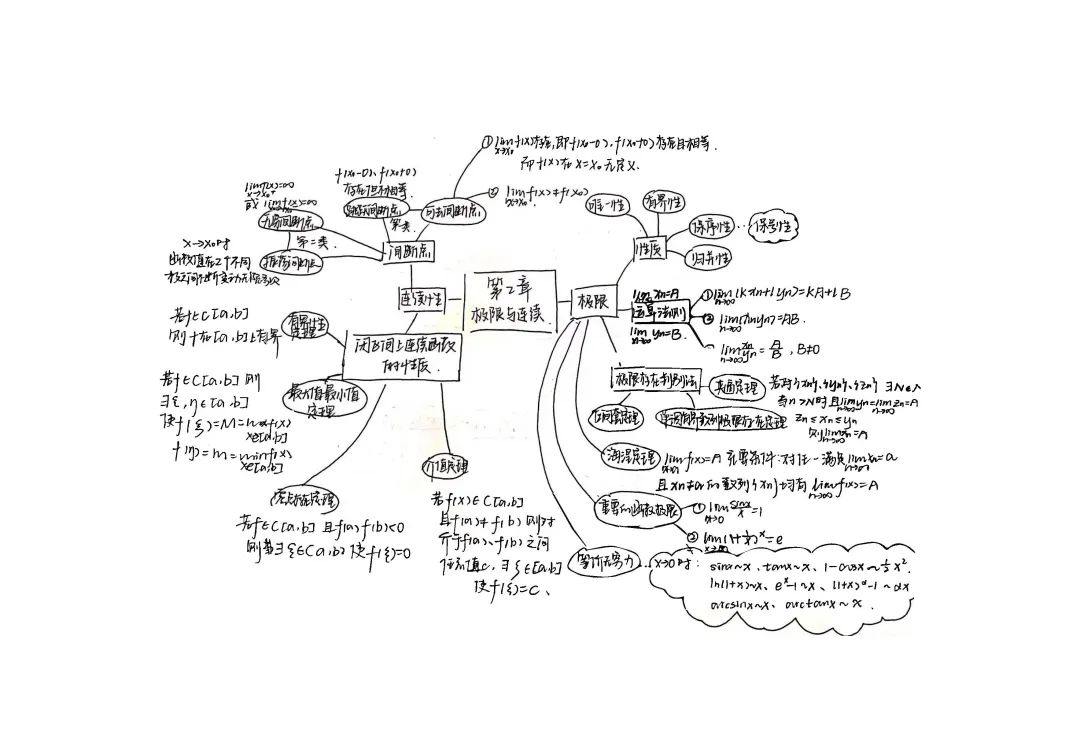
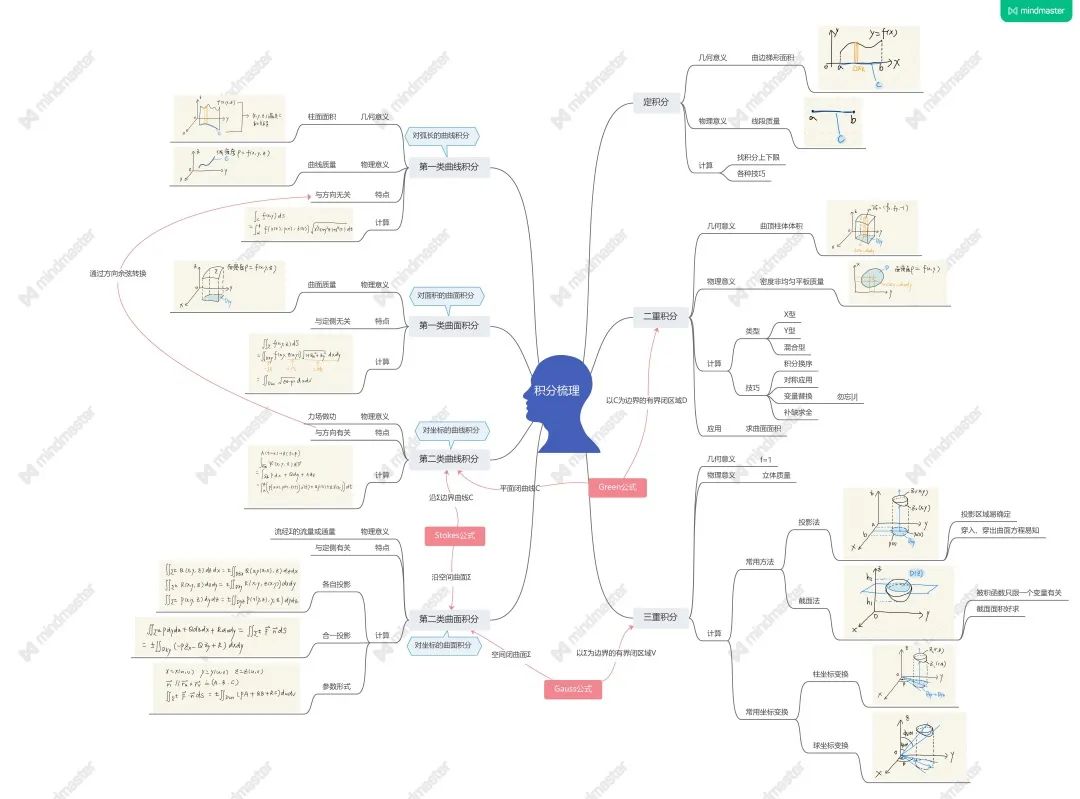
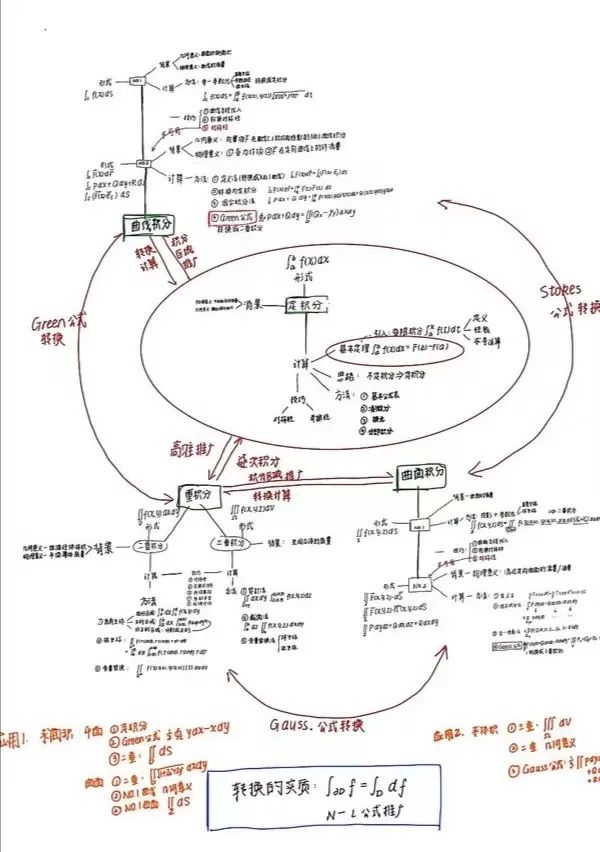
例如，大部分学生在高中阶段就接触了思维导图这一学习法，但是很多学生制作的思维导图仅仅停留在完善目录的层次上，缺乏深层次的思考、挖掘和建构。鉴于此，我在高数课上会进行三轮思维导图教学，将我所掌握的思维导图的整理方法和生成技巧都教给学生，要求他们提交多份思维导图作业，并对学生的思维导图作业进行点评。通过实施多轮思维导图的训练，增强了学生对知识结构的认知，也提升了学生的知识迁移和运用能力。

每次思维导图的作业反馈都显示出学生对这一学习任务超高的接受度和认可度，很多学生惊呼：

“太棒了！画了思维导图以后，知识结构格外清晰”

“整理时才发现原来自己已经学了这么多的知识和技巧”

“遗忘了很多，画思维导图一帧帧复习，效果真好”。

……

育人者必先育己，立己者方能立人。教师，要永远保持一个学习的心态，才能实施与时俱进的教育。教学既是一门科学,又是一门艺术，它既需要教师拥有扎实的专业知识功底，亦需要教师掌握先进的教学法。每位老师在读书时候所学知识并不足以支撑所有的教学工作，且教学理念、教学方法、教学模式等并非是老师与生俱来的，这就决定了老师必须要不断学习，注重提升自己的认知水平，提高教学技能，才能有效地开展教学工作。

我通过学校教学发展中心组织的系列活动学到了很多教学相关的理论和技术，对我的教学确实很有帮助。例如，一次关于“脑科学”的培训中讲到：研究表明，单纯的理论教学效果仅有28%，只讲例子的情况下教学效果不足20%，若是讲一个理论加两个例子，教学有效率可达62%。这一研究结论给了我重要的启示，在后续的教学中便以此为理论指导对教学过程进行了优化。作为一线教师，我们需要通过更新自己的教学理念、掌握先进的教学规律、学习科学的教学方法来提高自身的教育智慧，为培养新时代人才贡献力量。

18年的从教生涯，让我从当初那个稚嫩的“青椒”成长为一个在三尺讲台上游刃有余的成熟教师。我深刻感觉到时代的变化，学校在变，老师在变，学生也在变，但也有一些永恒的东西存在着，那就是数学的温度、年轻学子的好奇心与求知欲。希望我能够永葆自己的教育情怀，践行自己的教学理念，走近学生，尊重数学，潜心教学，做一个有温度、有情怀的数学老师。这即是我所追求的“永恒”精神。